Page 141
The injective dimension of a noetherian local ring is either infinite or equal to its dimension
Page 143
Since dim B=0, it's artinian and we can talk about its minimal ideals. Such an ideal is principal of the form but (0:b) is a maximal ideal because Bb has no submodule (B is a quotient of A and (0:b) is a quotient of m) therefore it's isomorphic to k.
Page 144
B is Artinian, so that 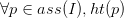 :
:
B is Artinian, so by a theorem in Sharp's book, a power of the maximal ideal annihilates the ring; hence the maximal ideal is a subset of zero devisors so belongs to Ass, therefore 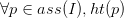 .
.